Problems in data science for SE

Neil Ernst

2025-07-29

Dataset Challenges in SE Data Science

What are the data sources?

Learning Objectives

Understand sources of software data.
Model the chance of finding an effect of interest.
Explore the limitations of software datasets.
Categorize sources of error in software research.

Data Sources

Commits
Issue trackers
Source code
Structured data
Stack Overflow
AI chat logs
…

What are some challenges?

Using the data that is available, instead of the data that answers the question.
Ignoring domain assumptions that produced the data, e.g. the human aspects (Secret Life of Bugs)
Sampling opportunistically (convenience) instead of systematically.
Not understanding the sensitivity of your instrument (the Kangaroo problem)
Questionable research practices

One of the biggest problems - and best places to spend money - is getting good data.

The most obvious example of this is building bigger telescopes or high energy physics instruments.

Example

Suppose I want to know how productive AI is making software developers.
I decide to run a controlled experiment: we will compare developers in two groups, with and without AI.
How should I go about doing this study?
Crossover - use the tool, then don’t use it.
Population inferences - are my groups random?
Say I use 4th year students?

Inference (review!)

What are we trying to accomplish? We would like some confidence that our experiment will reveal some true effect in the world.

The traditional frequentist (STAT260) approach is null-hypothesis significance testing (NHST) with p-values. ¹

Inference (2)

We run a test calculating the probability of the observed difference or a more extreme difference, under the assumption that there is no real difference between the groups.

We want a test that can find such a difference if it exists (else FN, type 2 error), and not find the difference if it does not exist (else FP, type 1 error).

NB: A non-significant p-value does not mean that the null hypothesis is true.

An example

Let’s get people to solve bugs with AI and without AI. Which one will be quicker to fix bugs? Our null hypothesis might be that it won’t matter. Our alternative might be that it does matter.

We can do some statistical testing to see which hypothesis might best explain the data. In the conventional framework, we would assume the null is true, and see if it continues to explain the numbers we see from doing the experiment (in this case, how fast bugs are fixed).

Example - R code

Load the two sample files into R, and run a t-test to evaluate the hypothesis that AI makes developers faster. Make sure to print out the descriptive stats first.

Long Break

Example - conclusions

If the data seem really unlikely under the null model, i.e., the AI users are nearly always slower, then we can reject the null.

We will need to define expected effect size, power of detecting that effect, and the threshold \(\alpha\) at which we reject the null.

Note: not the same as practical significance: A study might have statistical relevance but not practical. Can you think of examples?

Effect sizes (briefly)

Still need to connect statistical outcomes (difference of means) to real-world impact – practical significance.
E.g. Cliff’s D, \(R^2\) (explained variance), Cohen’s d, etc.

Effect sizes

from Section 2.3 of my paper:

“effect size ignores the context of decision making. A raw number reflecting (for example) the standardized difference of means is hard for practitioners to interpret and must be contextualized. Contextual, subjective judgment of observed effect sizes must be made and a ritualized interpretation avoided

Power Analysis

Power is the probability before a study is done that it will achieve statistical significance for \(\alpha < 0.05\) (or other values).
First, we guess an “effect size” for our test (e.g., difference of means), then guess at sample size and variation.
Most funders would expect studies to have power > 80%.
Power analysis is inherently exploratory and hypothetical - simulation can help.
What about study costs? Maybe it is cheap to collect data.

Power example

Visit here:

Noisy data

when noise is high and signal is low, statistically significant results are unlikely to replicate.
type M - magnitude and type S - sign errors more likely in low-powered studies
Best approach is to design a study to maximize effect size rather than population
E.g., look at groups more likely to respond, increase treatment amounts
Everything has an effect!

Secret Life of Bugs

What is the “secret”?

The histories of even simple bugs are strongly dependent on social, organizational, and technical knowledge that cannot be solely extracted through automation of electronic repositories

Levels

Bug record data: bug tracker, resolution, people involved, commits associated
Automated conversation analysis: examining comments
Sense-making by informed observer
Direct narrative reports by participants

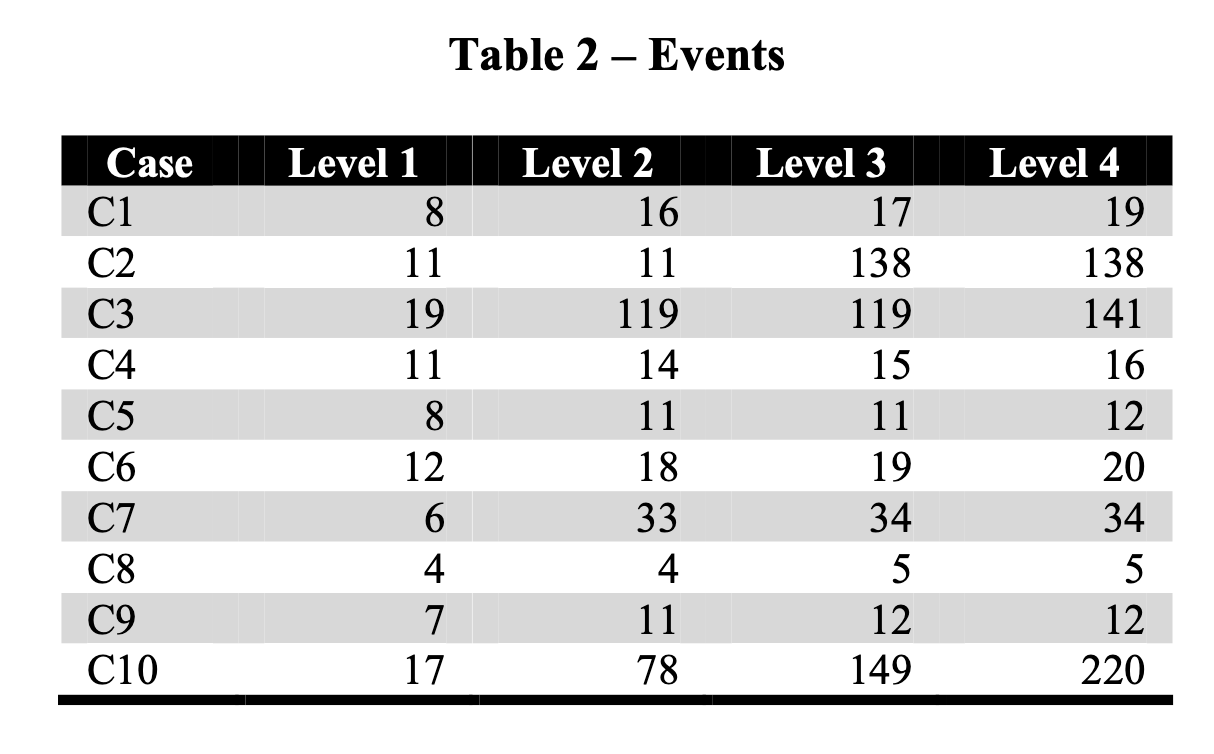
Stark differences in data available

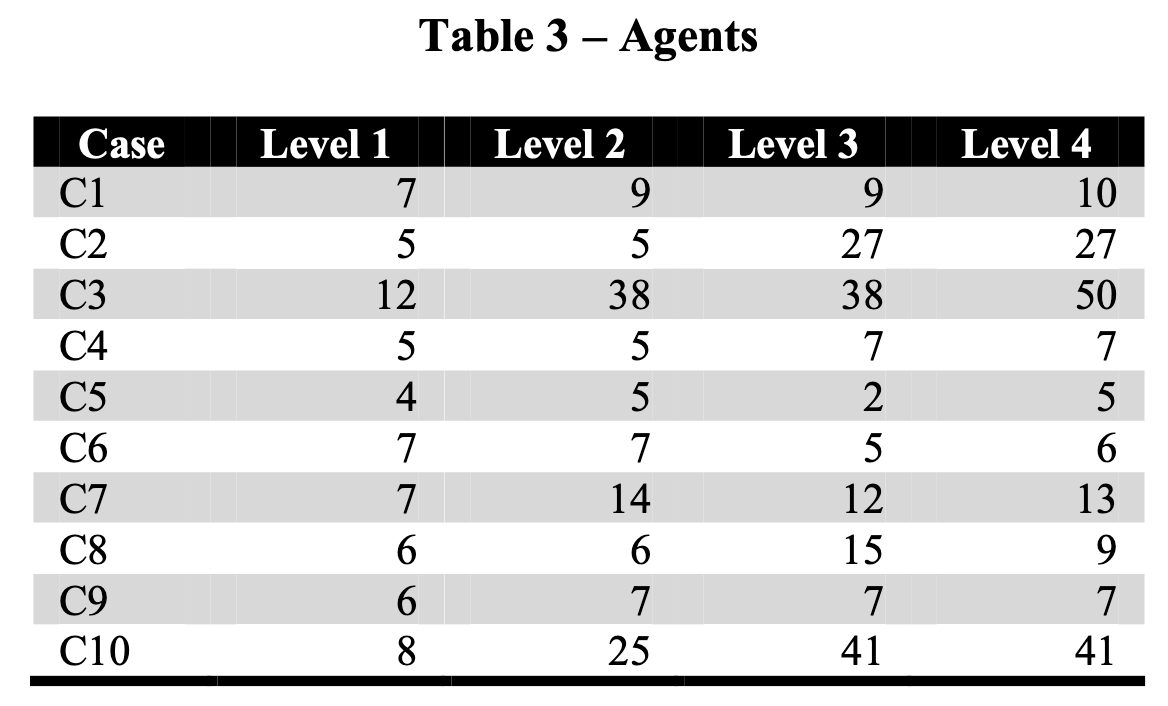
number of people involved

Number of events

Sampling

For many SE phenomena, there is no suitable sampling frame; that is, a list from which to draw a sample.
Some SE studies adopt poorly understood sampling strategies such as random sampling from a non-representative surrogate population.
Many SE articles evince deep misunderstandings of representativeness—the key criteria for assessing sampling in positivist research (see Section 2.6).

Sampling Approaches

Convenience
Purposive
Snowball
Probabilistic (random)
1. Simple
2. Stratified

Sampling Challenges

Finding a representative sample: representativeness is the degree to which a sample’s properties (of interest) resemble those of a target population
Randomness is not sufficient
Some philosophies do not view representativeness as desirable or relevant.
Software people are expensive
Real data is often under NDA
Software projects cover a vast universe of domains and contexts

Bad Smells in Software Samples

Arguing that a convenience sample of software projects is representative because they are “real-world” projects.
Incorrectly using the term “random” to mean arbitrary.
Assuming that a small sample is representative because it is random.
Assuming that a large random sample is representative despite being selected from an obviously biased sampling frame.
Implying that results should generalize to large populations without any claim to having a representative sample.

Exercise

Design a sampling strategy for the following question:

You are the manager of 10 teams at Spotify doing software development. Each team uses their own tools; some use Slack, others use email and IRC. Is there a connection between Slack use and team reported productivity?

and

You are looking to see how many bugs exist in primarily machine-learning software (e.g., building and training ML models with Tensorflow) vs other types of software

Git Promises and Perils

promises: analysis Git enables
perils: dangers with relying on Git in general: the data we see may not be an impartial log of events

Perils

Git new on the scene at the time (replacing SVN/CVS)
Git is distributed
Git histories can be cleaned
- delete/omit commits, squash / condense commits into one
- lose the rich history of how a change was arrived at
Git branches are potentially confusing

Github Promises and Perils

Repos =/= project (forks for PRs)
Many projects inactive or uninteresting
Some repos are for data storage or personal use
PRs used in different ways.
PRs don’t record all commits.
Most pull requests appear as non-merged even if they are actually merged.
Many active projects do not conduct all their software development in GitHub

Other Challenges

temporal pollution
likes and stars
bots
gender and demographics

Summary

Both statistics tools AND data acquisition have potential problems
Doing a high quality study supports our claims for practical significance
Good data science means paying close attention to:
- sampling approach
- experimental designs
- inferential tools
- potential problems and perils