Prior Probability Distributions

Selection and Discrimination

Neil Ernst
nernst@uvic.ca

University of Victoria

2025-07-29

Code 
library(tidyverse)

A short digression into priors

How should we choose our priors? Isn’t this biasing the inference?

We will set likelihoods using statistical probability distributions (in R type ?Distributions). These distributions cover a range of widely understood generative processes. Our priors will come from our choice of the parameters for these distributions.

Types of Priors

  • Gaussian/Normal distribution
  • Binomial
  • Uniform
  • Student’s T
  • Poisson
  • InvGamma
  • Weibull

And many many others.

Probability Distributions

A probability distribution maps an event (along the x-axis) to its probability of happening (a Probability Density Function, PDF).

Probabilities range from 0-1. A Cumulative Density Function (CDF) represents the cumulative probability, eventually approaching 1.

Distributions can be modeled mathematically - the above Wikipedia link details this. For the Normal distribution, for example, its PDF is represented as

\({\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}\)

and the parameters are \(\mu\), \(\sigma\), and data points x \(\in\) X.

Often our interest in a Bayesian context is recovering the location parameter \(\mu\) and the shape parameter \(\sigma\) of the posterior distribution.

Looking at Distributions in R

In R, these distributions are included by default, and can be used typically with the following prefixes:

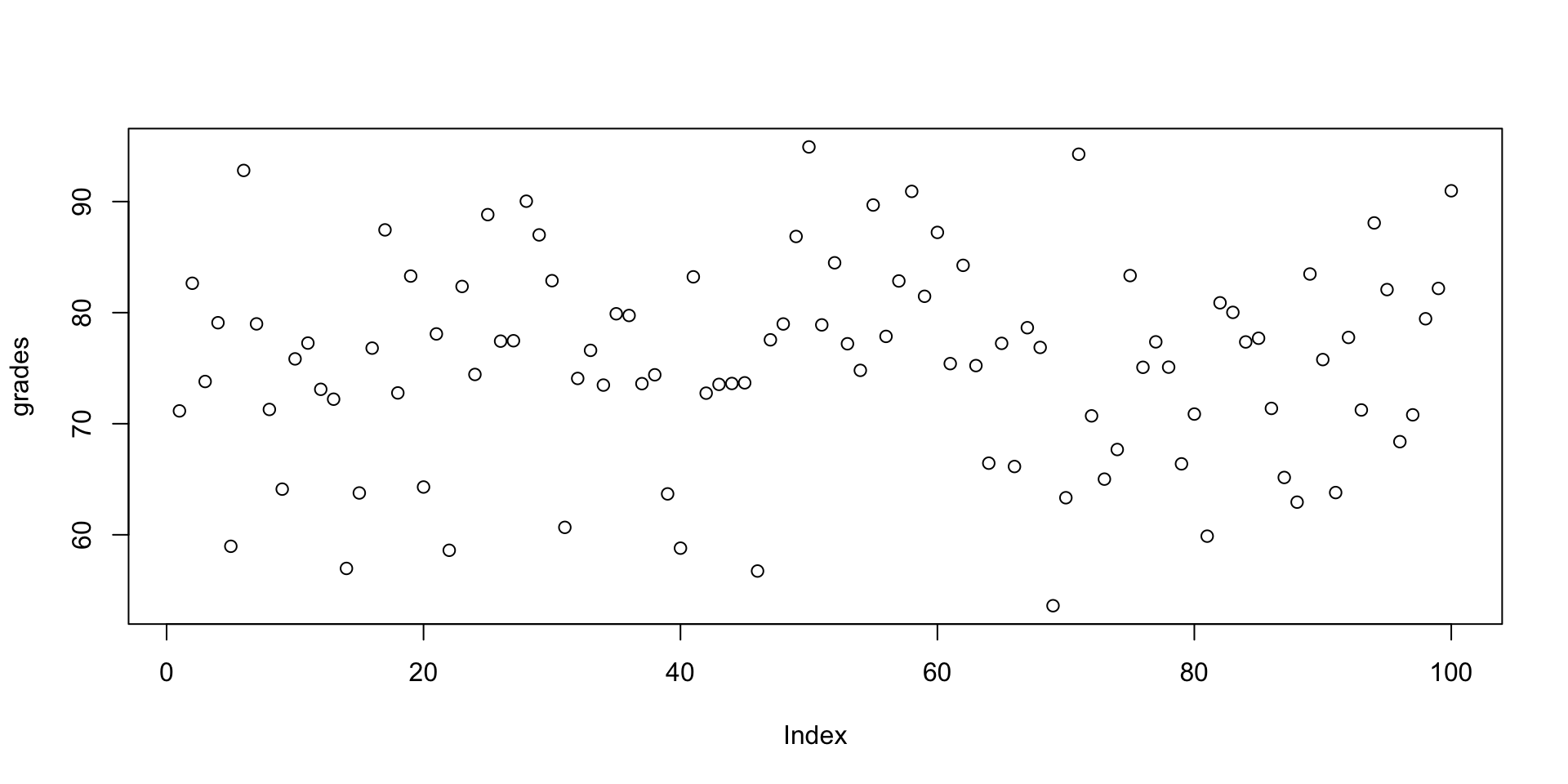
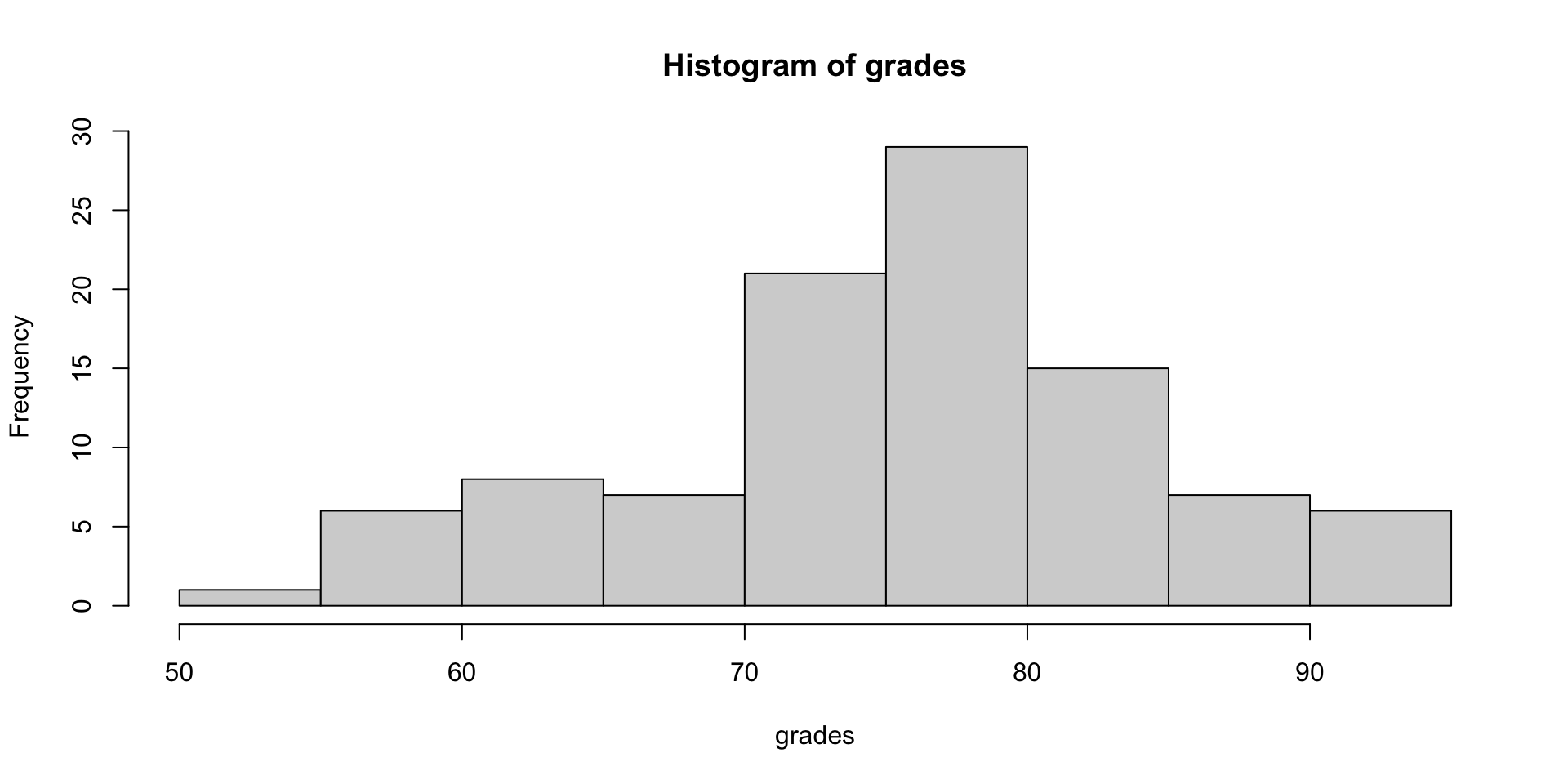
d, for “density”, r for “random generation” (ie. draw one number from the distribution at random), p for the distribution, q for quantile. To do a simulation of the grades of 100 students at random assuming the grades are normally distributed with \(\mu=\) 75 and \(\sigma\)=10, we could say

Sample code

Code 
grades = rnorm(100, 75, 10)
plot(grades)

Code 
hist(grades)

and get a vector of grades, again randomly distributed according to the parameterization we specified. (Hmm, new grading idea!)

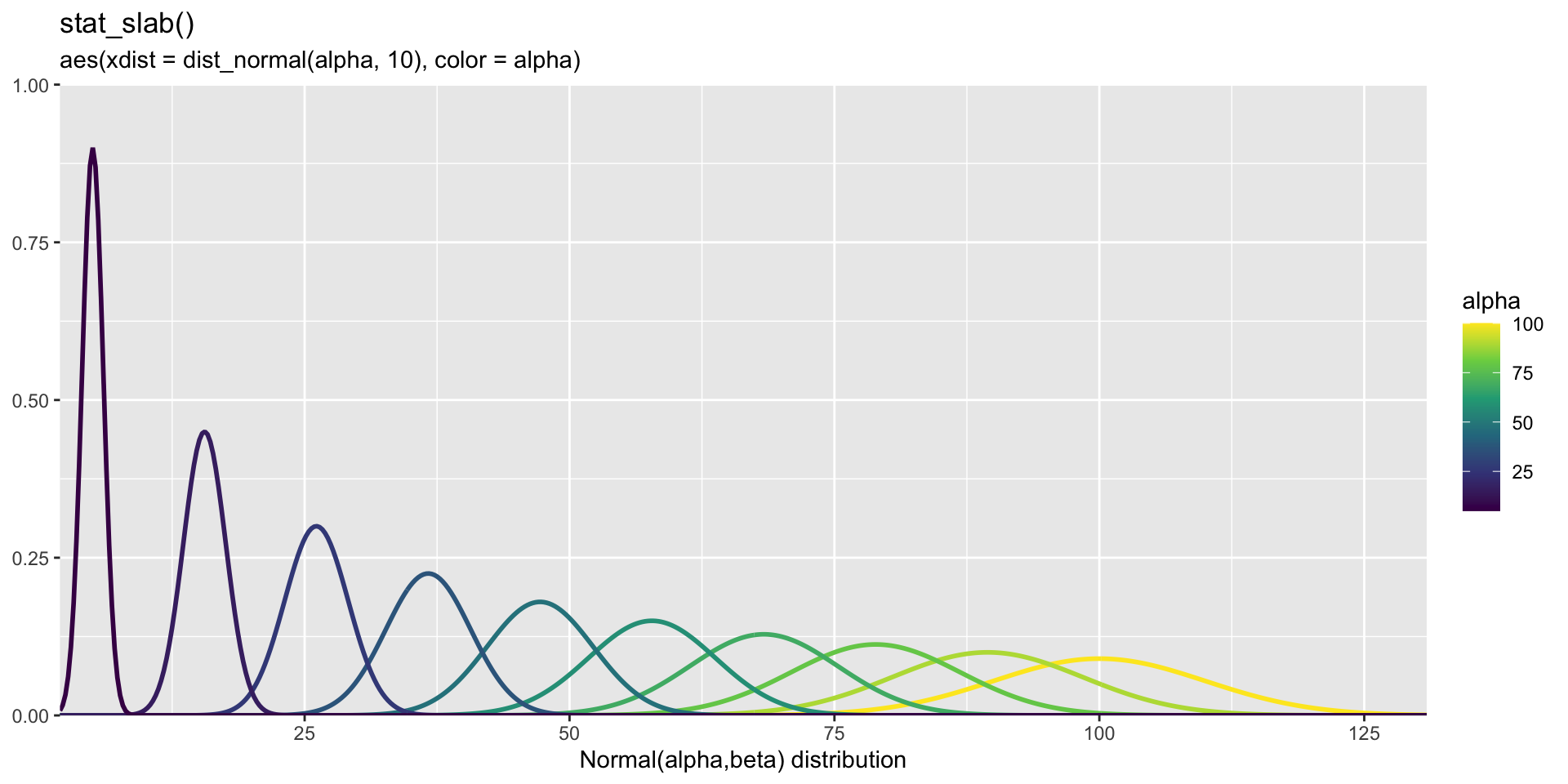
Playing with Distributions

Code 
library(ggdist)
library(distributional)
data.frame(alpha = seq(5, 100, length.out = 10), beta = seq(1,10,length.out=10)) %>%
  ggplot(aes(xdist = dist_normal(mu=alpha, sigma=beta), color = alpha)) +
  stat_slab(fill = NA) +
  coord_cartesian(expand = FALSE) +
  scale_color_viridis_c() +
  labs(
    title = "stat_slab()",
    subtitle = "aes(xdist = dist_normal(alpha, 10), color = alpha)",
    x = "Normal(alpha,beta) distribution",
    y = NULL
  )

Choosing A Prior

One thing to note: libraries like fitdistrplus allow you to fit distributions to the data (in this case, using maximum likelihood density estimation to ‘smooth’ the underlying probability density).

There are other tests to measure if the distribution you choose matches the data well, such as QQ plots. Just because the data isn’t normally distributed (Gaussian) doesn’t mean there isn’t some underlying generative function behind it.

Code 
# from https://cran.r-project.org/web/packages/fitdistrplus/vignettes/fitdistrplus_vignette.html

# install.packages("fitdistrplus")

library(fitdistrplus)
data("groundbeef")
# fit <- fitdist(groundbeef, distr = "gamma", method = "mle")
plotdist(groundbeef$serving, histo = TRUE, demp = TRUE)

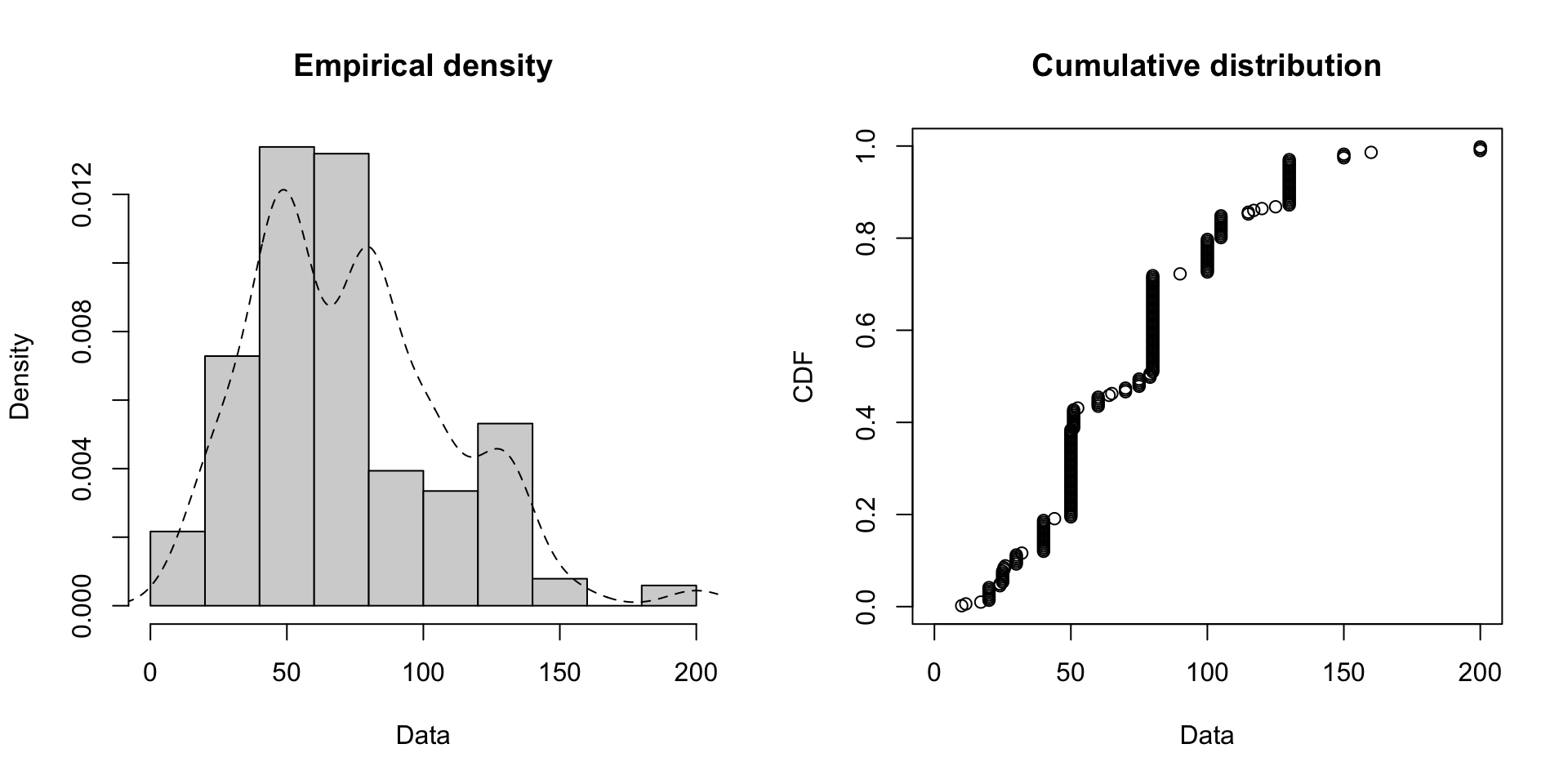
Code 
par(mfrow = c(1, 1), mar = c(4, 4, 2, 1))
plot.legend <- c("Weibull", "lognormal", "gamma")
# three different distributions we can check
fw <- fitdist(groundbeef$serving, "weibull")
fg <- fitdist(groundbeef$serving, "gamma")
fln <- fitdist(groundbeef$serving, "lnorm")
denscomp(list(fw, fln, fg), legendtext = plot.legend)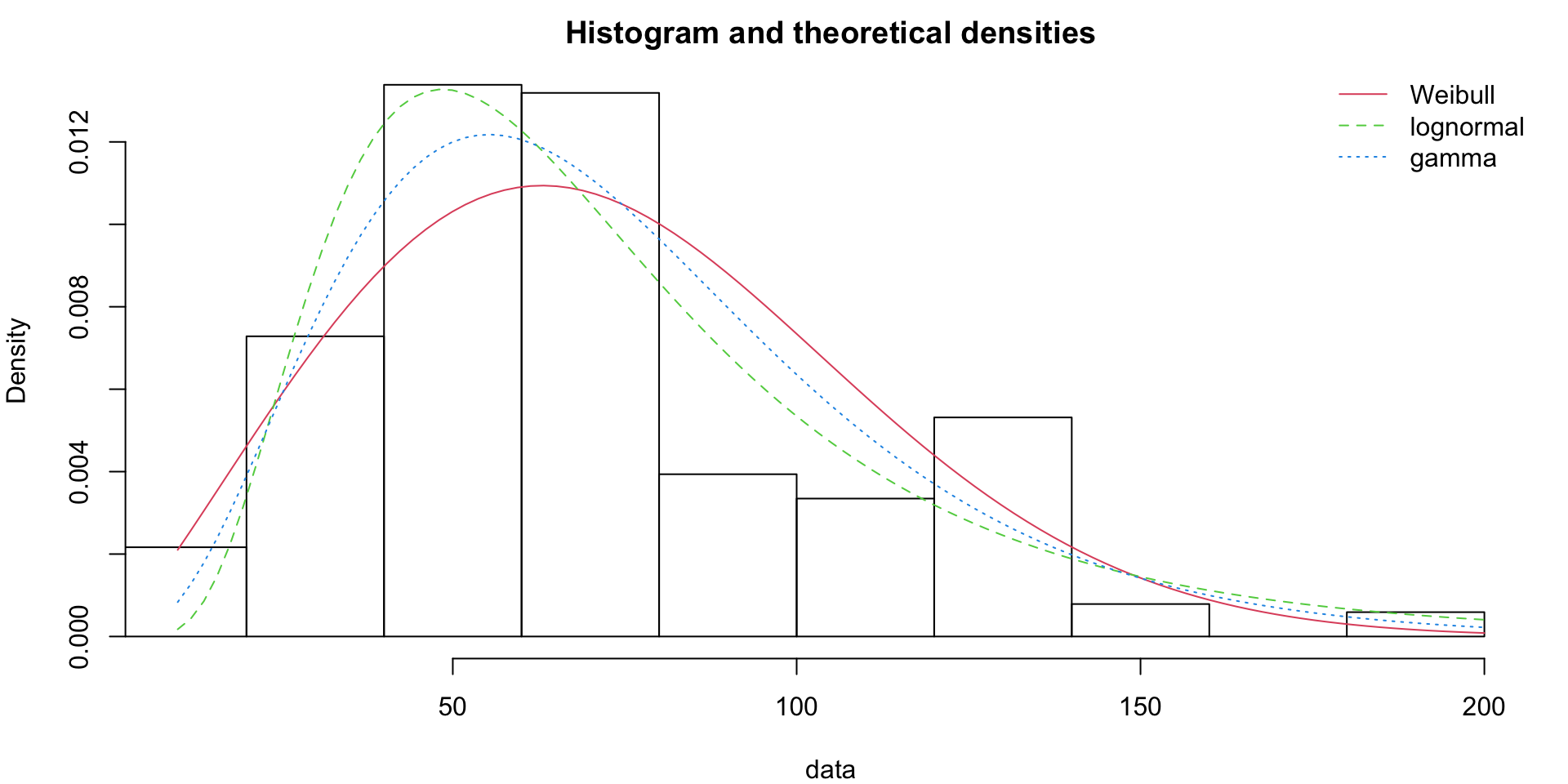

Choosing A Prior - Visualizing Distributions

A handy set of probability distributions

Choosing A Prior

  • This is fine in our inductive mode, but totally unacceptable in a deductive study. Why?
  • In a principled Bayesian workflow we would try to choose the prior based on our domain understanding first, perhaps basing this on what we have seen in similar research projects.

Weakly-informative, Uninformative, Opionated

A prior acts like a sea anchor or drogue chute on the engine of the data and likelihood.

Here’s a sea anchor:

Regularization

It regularizes the data fitting, essentially saying “sure, look at the data, but keep these biases in mind”. And yes, they are biases, but at least we are being explicit about them! And it makes sense; if we see strange data about how a particular project has Zero defects, we have two choices:

  1. what an amazing team! they have uniquely figured out how to write defect-free code.
  2. something is off; our data collection is not accounting for defects somehow.

In the case of (2) we need to assign a bias that explains how we expect defects to occur.

Basic Choices

We have three choices.

  1. uninformative prior: we don’t know what to expect (1). Don’t let the prior affect our posterior output at all. This is almost certainly not the case.
  2. opionated prior: we have a very strong belief in what the output should look like. Only very extreme data should change this. This might be true if, for example, we were working with laws of physics like the gravitational constant.
  3. weakly informative prior: the Goldilocks choice, these priors give a range of expected outputs, but within those parameters, the output can change dramatically. For example, we know each file has to have greater than or equal to zero defects. Getting a value of -1 in the output predictions would be an error. We can improve our inferences by making that clear.

Playing with Choices

Here are the three choices, after I ran simple inference with Stan. See also ?rstanarm::priors

First, the flat prior on the wt parameter. This data is from mtcars, a built-in dataset about cars and weight, miles per gallon (mpg), etc.

Code 
library(rstanarm)
m1 <- 'mpg ~ wt'
mean(mtcars$mpg) # 20.091
flat_prior_test <- stan_glm(m1, family=gaussian, data=mtcars, prior=NULL)

Code 
prior_summary(flat_prior_test)
Code 
pp_check(flat_prior_test)

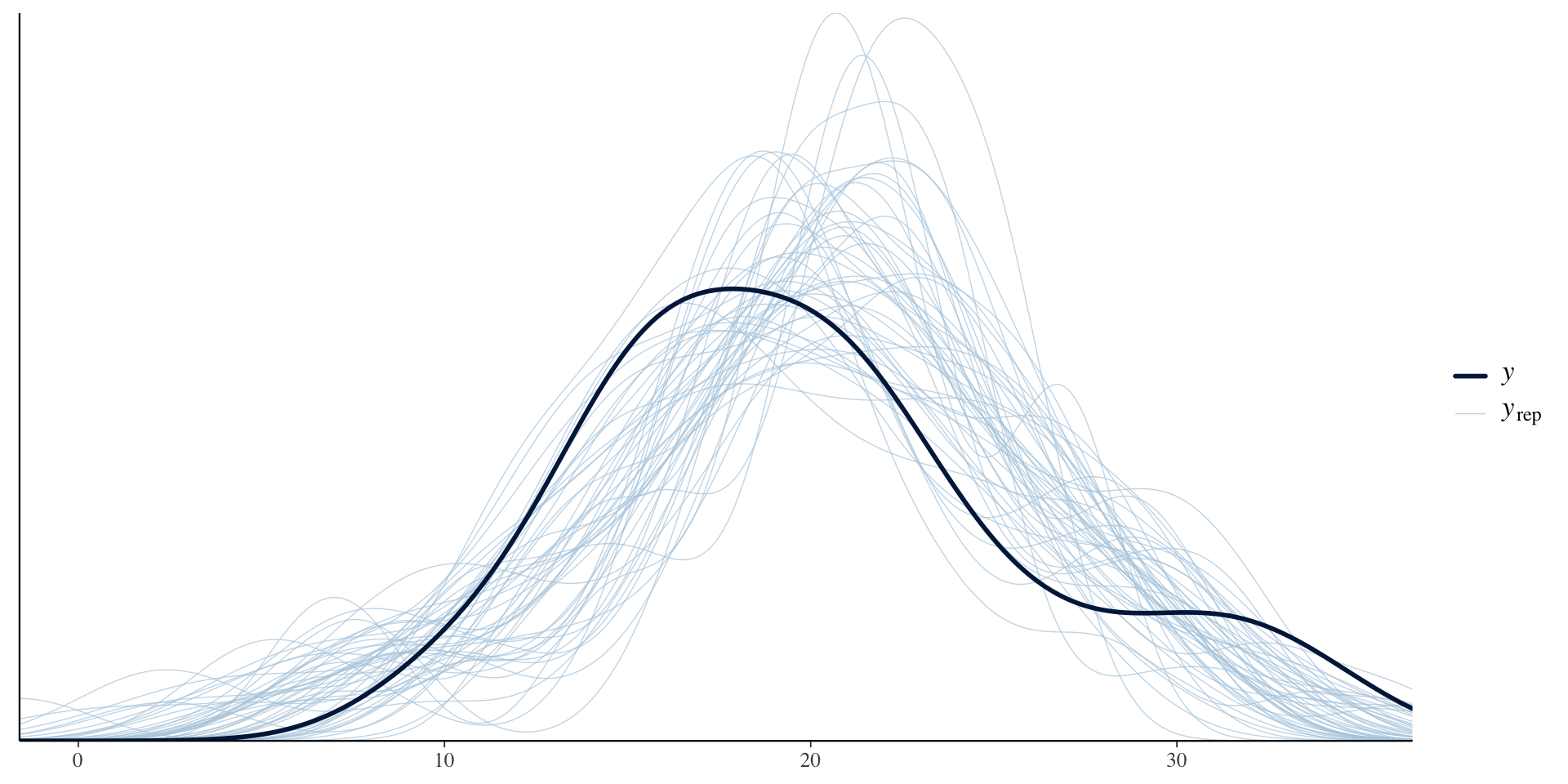
Priors for model 'flat_prior_test' 
------
Intercept (after predictors centered)
  Specified prior:
    ~ normal(location = 20, scale = 2.5)
  Adjusted prior:
    ~ normal(location = 20, scale = 15)

Coefficients
 ~ flat

Auxiliary (sigma)
  Specified prior:
    ~ exponential(rate = 1)
  Adjusted prior:
    ~ exponential(rate = 0.17)
------
See help('prior_summary.stanreg') for more details

Code 
# same model
weak_prior_test <- stan_glm(m1, family=gaussian, data=mtcars)

SAMPLING FOR MODEL 'continuous' NOW (CHAIN 1).
Chain 1: 
Chain 1: Gradient evaluation took 5.7e-05 seconds
Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.57 seconds.
Chain 1: Adjust your expectations accordingly!
Chain 1: 
Chain 1: 
Chain 1: Iteration:    1 / 2000 [  0%]  (Warmup)
Chain 1: Iteration:  200 / 2000 [ 10%]  (Warmup)
Chain 1: Iteration:  400 / 2000 [ 20%]  (Warmup)
Chain 1: Iteration:  600 / 2000 [ 30%]  (Warmup)
Chain 1: Iteration:  800 / 2000 [ 40%]  (Warmup)
Chain 1: Iteration: 1000 / 2000 [ 50%]  (Warmup)
Chain 1: Iteration: 1001 / 2000 [ 50%]  (Sampling)
Chain 1: Iteration: 1200 / 2000 [ 60%]  (Sampling)
Chain 1: Iteration: 1400 / 2000 [ 70%]  (Sampling)
Chain 1: Iteration: 1600 / 2000 [ 80%]  (Sampling)
Chain 1: Iteration: 1800 / 2000 [ 90%]  (Sampling)
Chain 1: Iteration: 2000 / 2000 [100%]  (Sampling)
Chain 1: 
Chain 1:  Elapsed Time: 0.014 seconds (Warm-up)
Chain 1:                0.014 seconds (Sampling)
Chain 1:                0.028 seconds (Total)
Chain 1: 

SAMPLING FOR MODEL 'continuous' NOW (CHAIN 2).
Chain 2: 
Chain 2: Gradient evaluation took 3e-06 seconds
Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0.03 seconds.
Chain 2: Adjust your expectations accordingly!
Chain 2: 
Chain 2: 
Chain 2: Iteration:    1 / 2000 [  0%]  (Warmup)
Chain 2: Iteration:  200 / 2000 [ 10%]  (Warmup)
Chain 2: Iteration:  400 / 2000 [ 20%]  (Warmup)
Chain 2: Iteration:  600 / 2000 [ 30%]  (Warmup)
Chain 2: Iteration:  800 / 2000 [ 40%]  (Warmup)
Chain 2: Iteration: 1000 / 2000 [ 50%]  (Warmup)
Chain 2: Iteration: 1001 / 2000 [ 50%]  (Sampling)
Chain 2: Iteration: 1200 / 2000 [ 60%]  (Sampling)
Chain 2: Iteration: 1400 / 2000 [ 70%]  (Sampling)
Chain 2: Iteration: 1600 / 2000 [ 80%]  (Sampling)
Chain 2: Iteration: 1800 / 2000 [ 90%]  (Sampling)
Chain 2: Iteration: 2000 / 2000 [100%]  (Sampling)
Chain 2: 
Chain 2:  Elapsed Time: 0.013 seconds (Warm-up)
Chain 2:                0.012 seconds (Sampling)
Chain 2:                0.025 seconds (Total)
Chain 2: 

SAMPLING FOR MODEL 'continuous' NOW (CHAIN 3).
Chain 3: 
Chain 3: Gradient evaluation took 2e-06 seconds
Chain 3: 1000 transitions using 10 leapfrog steps per transition would take 0.02 seconds.
Chain 3: Adjust your expectations accordingly!
Chain 3: 
Chain 3: 
Chain 3: Iteration:    1 / 2000 [  0%]  (Warmup)
Chain 3: Iteration:  200 / 2000 [ 10%]  (Warmup)
Chain 3: Iteration:  400 / 2000 [ 20%]  (Warmup)
Chain 3: Iteration:  600 / 2000 [ 30%]  (Warmup)
Chain 3: Iteration:  800 / 2000 [ 40%]  (Warmup)
Chain 3: Iteration: 1000 / 2000 [ 50%]  (Warmup)
Chain 3: Iteration: 1001 / 2000 [ 50%]  (Sampling)
Chain 3: Iteration: 1200 / 2000 [ 60%]  (Sampling)
Chain 3: Iteration: 1400 / 2000 [ 70%]  (Sampling)
Chain 3: Iteration: 1600 / 2000 [ 80%]  (Sampling)
Chain 3: Iteration: 1800 / 2000 [ 90%]  (Sampling)
Chain 3: Iteration: 2000 / 2000 [100%]  (Sampling)
Chain 3: 
Chain 3:  Elapsed Time: 0.013 seconds (Warm-up)
Chain 3:                0.016 seconds (Sampling)
Chain 3:                0.029 seconds (Total)
Chain 3: 

SAMPLING FOR MODEL 'continuous' NOW (CHAIN 4).
Chain 4: 
Chain 4: Gradient evaluation took 2e-06 seconds
Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 0.02 seconds.
Chain 4: Adjust your expectations accordingly!
Chain 4: 
Chain 4: 
Chain 4: Iteration:    1 / 2000 [  0%]  (Warmup)
Chain 4: Iteration:  200 / 2000 [ 10%]  (Warmup)
Chain 4: Iteration:  400 / 2000 [ 20%]  (Warmup)
Chain 4: Iteration:  600 / 2000 [ 30%]  (Warmup)
Chain 4: Iteration:  800 / 2000 [ 40%]  (Warmup)
Chain 4: Iteration: 1000 / 2000 [ 50%]  (Warmup)
Chain 4: Iteration: 1001 / 2000 [ 50%]  (Sampling)
Chain 4: Iteration: 1200 / 2000 [ 60%]  (Sampling)
Chain 4: Iteration: 1400 / 2000 [ 70%]  (Sampling)
Chain 4: Iteration: 1600 / 2000 [ 80%]  (Sampling)
Chain 4: Iteration: 1800 / 2000 [ 90%]  (Sampling)
Chain 4: Iteration: 2000 / 2000 [100%]  (Sampling)
Chain 4: 
Chain 4:  Elapsed Time: 0.013 seconds (Warm-up)
Chain 4:                0.013 seconds (Sampling)
Chain 4:                0.026 seconds (Total)
Chain 4:
Code 
prior_summary(weak_prior_test)
Priors for model 'weak_prior_test' 
------
Intercept (after predictors centered)
  Specified prior:
    ~ normal(location = 20, scale = 2.5)
  Adjusted prior:
    ~ normal(location = 20, scale = 15)

Coefficients
  Specified prior:
    ~ normal(location = 0, scale = 2.5)
  Adjusted prior:
    ~ normal(location = 0, scale = 15)

Auxiliary (sigma)
  Specified prior:
    ~ exponential(rate = 1)
  Adjusted prior:
    ~ exponential(rate = 0.17)
------
See help('prior_summary.stanreg') for more details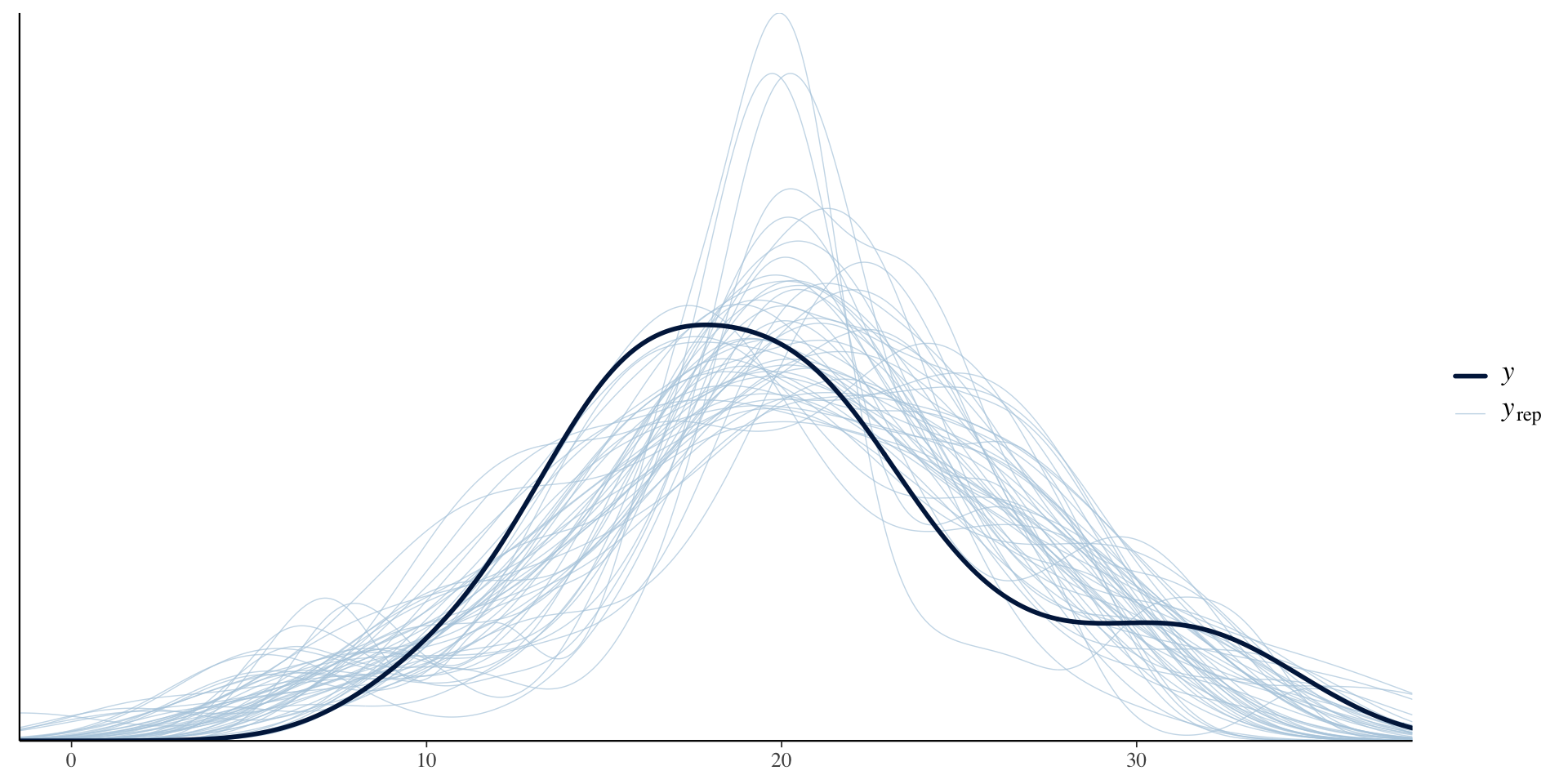
Code 
pp_check(weak_prior_test)

Code 
strong_prior_test <- stan_glm(m1, family=gaussian, data=mtcars)

SAMPLING FOR MODEL 'continuous' NOW (CHAIN 1).
Chain 1: 
Chain 1: Gradient evaluation took 1.3e-05 seconds
Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 0.13 seconds.
Chain 1: Adjust your expectations accordingly!
Chain 1: 
Chain 1: 
Chain 1: Iteration:    1 / 2000 [  0%]  (Warmup)
Chain 1: Iteration:  200 / 2000 [ 10%]  (Warmup)
Chain 1: Iteration:  400 / 2000 [ 20%]  (Warmup)
Chain 1: Iteration:  600 / 2000 [ 30%]  (Warmup)
Chain 1: Iteration:  800 / 2000 [ 40%]  (Warmup)
Chain 1: Iteration: 1000 / 2000 [ 50%]  (Warmup)
Chain 1: Iteration: 1001 / 2000 [ 50%]  (Sampling)
Chain 1: Iteration: 1200 / 2000 [ 60%]  (Sampling)
Chain 1: Iteration: 1400 / 2000 [ 70%]  (Sampling)
Chain 1: Iteration: 1600 / 2000 [ 80%]  (Sampling)
Chain 1: Iteration: 1800 / 2000 [ 90%]  (Sampling)
Chain 1: Iteration: 2000 / 2000 [100%]  (Sampling)
Chain 1: 
Chain 1:  Elapsed Time: 0.014 seconds (Warm-up)
Chain 1:                0.014 seconds (Sampling)
Chain 1:                0.028 seconds (Total)
Chain 1: 

SAMPLING FOR MODEL 'continuous' NOW (CHAIN 2).
Chain 2: 
Chain 2: Gradient evaluation took 5e-06 seconds
Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0.05 seconds.
Chain 2: Adjust your expectations accordingly!
Chain 2: 
Chain 2: 
Chain 2: Iteration:    1 / 2000 [  0%]  (Warmup)
Chain 2: Iteration:  200 / 2000 [ 10%]  (Warmup)
Chain 2: Iteration:  400 / 2000 [ 20%]  (Warmup)
Chain 2: Iteration:  600 / 2000 [ 30%]  (Warmup)
Chain 2: Iteration:  800 / 2000 [ 40%]  (Warmup)
Chain 2: Iteration: 1000 / 2000 [ 50%]  (Warmup)
Chain 2: Iteration: 1001 / 2000 [ 50%]  (Sampling)
Chain 2: Iteration: 1200 / 2000 [ 60%]  (Sampling)
Chain 2: Iteration: 1400 / 2000 [ 70%]  (Sampling)
Chain 2: Iteration: 1600 / 2000 [ 80%]  (Sampling)
Chain 2: Iteration: 1800 / 2000 [ 90%]  (Sampling)
Chain 2: Iteration: 2000 / 2000 [100%]  (Sampling)
Chain 2: 
Chain 2:  Elapsed Time: 0.012 seconds (Warm-up)
Chain 2:                0.013 seconds (Sampling)
Chain 2:                0.025 seconds (Total)
Chain 2: 

SAMPLING FOR MODEL 'continuous' NOW (CHAIN 3).
Chain 3: 
Chain 3: Gradient evaluation took 2e-06 seconds
Chain 3: 1000 transitions using 10 leapfrog steps per transition would take 0.02 seconds.
Chain 3: Adjust your expectations accordingly!
Chain 3: 
Chain 3: 
Chain 3: Iteration:    1 / 2000 [  0%]  (Warmup)
Chain 3: Iteration:  200 / 2000 [ 10%]  (Warmup)
Chain 3: Iteration:  400 / 2000 [ 20%]  (Warmup)
Chain 3: Iteration:  600 / 2000 [ 30%]  (Warmup)
Chain 3: Iteration:  800 / 2000 [ 40%]  (Warmup)
Chain 3: Iteration: 1000 / 2000 [ 50%]  (Warmup)
Chain 3: Iteration: 1001 / 2000 [ 50%]  (Sampling)
Chain 3: Iteration: 1200 / 2000 [ 60%]  (Sampling)
Chain 3: Iteration: 1400 / 2000 [ 70%]  (Sampling)
Chain 3: Iteration: 1600 / 2000 [ 80%]  (Sampling)
Chain 3: Iteration: 1800 / 2000 [ 90%]  (Sampling)
Chain 3: Iteration: 2000 / 2000 [100%]  (Sampling)
Chain 3: 
Chain 3:  Elapsed Time: 0.012 seconds (Warm-up)
Chain 3:                0.013 seconds (Sampling)
Chain 3:                0.025 seconds (Total)
Chain 3: 

SAMPLING FOR MODEL 'continuous' NOW (CHAIN 4).
Chain 4: 
Chain 4: Gradient evaluation took 2e-06 seconds
Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 0.02 seconds.
Chain 4: Adjust your expectations accordingly!
Chain 4: 
Chain 4: 
Chain 4: Iteration:    1 / 2000 [  0%]  (Warmup)
Chain 4: Iteration:  200 / 2000 [ 10%]  (Warmup)
Chain 4: Iteration:  400 / 2000 [ 20%]  (Warmup)
Chain 4: Iteration:  600 / 2000 [ 30%]  (Warmup)
Chain 4: Iteration:  800 / 2000 [ 40%]  (Warmup)
Chain 4: Iteration: 1000 / 2000 [ 50%]  (Warmup)
Chain 4: Iteration: 1001 / 2000 [ 50%]  (Sampling)
Chain 4: Iteration: 1200 / 2000 [ 60%]  (Sampling)
Chain 4: Iteration: 1400 / 2000 [ 70%]  (Sampling)
Chain 4: Iteration: 1600 / 2000 [ 80%]  (Sampling)
Chain 4: Iteration: 1800 / 2000 [ 90%]  (Sampling)
Chain 4: Iteration: 2000 / 2000 [100%]  (Sampling)
Chain 4: 
Chain 4:  Elapsed Time: 0.012 seconds (Warm-up)
Chain 4:                0.014 seconds (Sampling)
Chain 4:                0.026 seconds (Total)
Chain 4:
Code 
prior_summary(strong_prior_test)
Priors for model 'strong_prior_test' 
------
Intercept (after predictors centered)
  Specified prior:
    ~ normal(location = 20, scale = 2.5)
  Adjusted prior:
    ~ normal(location = 20, scale = 15)

Coefficients
  Specified prior:
    ~ normal(location = 0, scale = 2.5)
  Adjusted prior:
    ~ normal(location = 0, scale = 15)

Auxiliary (sigma)
  Specified prior:
    ~ exponential(rate = 1)
  Adjusted prior:
    ~ exponential(rate = 0.17)
------
See help('prior_summary.stanreg') for more details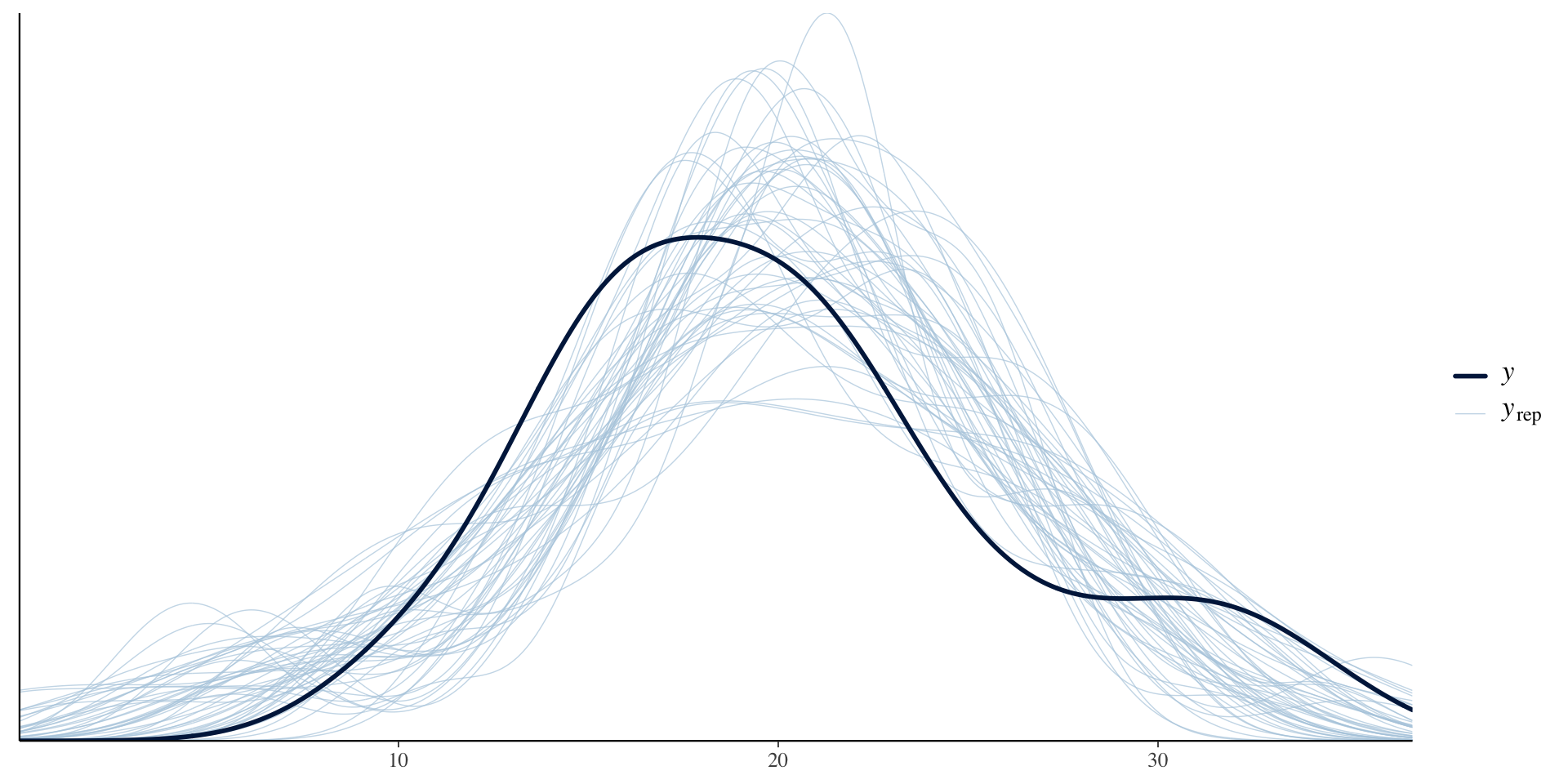
Code 
pp_check(strong_prior_test)

In other words, taking the data and fitting a distribution implies we think the data perfectly determines the distribution. This may not be (and often isn’t) the case.

For the purposes of this course the defaults will be fine.

One of the bigger challenges for non-statisticians like us is understanding the underlying assumptions and applicability of probability distributions. In a lot of cases the Normal, Poisson, logNormal distributions (in addition to Uniform) give us most of what we need for this course.

Simple Prior Choices

  • The Poisson is good for simulating discrete event arrivals, like bugs in code or cars at a stoplight.
  • The logNormal simulates the possibility that there is a fat tail (skewness) in the data, which is often the case in software data (especially for networks). Of course we could take the log of the measured data that is logNormally distributed and then model the result using the simple Normal distribution.
  • The Uniform is an equal probability distribution across all outcomes, and often models the situation when we don’t know any better.

Effect of prior on data (and vice-versa)